Vector or Cross Product of Two Vectors

#. Vector or Cross Product of Two Vectors :

The vector product of two vectors is equal to the product of their magnitudes and the sine of the smaller angle between them. It is denoted by * (cross).

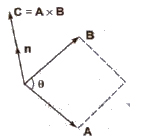
A * B = AB sin θ n

The direction of unit vector n can be obtained from right hand thumb rule.

If fingers of right hand are curled from A to B through smaller angle between them, then thumb will represent the direction of vector (A * B).

The vector or cross product of two vectors is also a vector.

#. Properties of Vector Product :

(i) Vector product is not commutative, i.e.,

A * B ≠ B * A  [∴ (A * B) = — (B * A)]

(ii) Vector product is distributive, i.e.,

A * (B + C) = A * B + A * C

(iii) Vector product of two parallel vectors is zero, i.e.,

A * B = AB sin O° = 0

(iv) Vector product of any vector with itself is zero.

A * A = AA sin O° = 0

(v) Vector product of orthogonal unit vectors

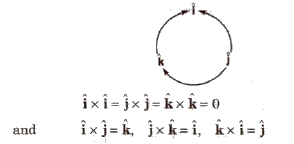
(vi) Vector product in cartesian coordinates

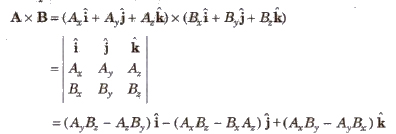
#. Direction of Vector Cross Product :

When C = A * B, the direction of C is at right angles to the plane containing the vectors A and B. The direction is determined by the right hand screw rule and right hand thumb rule.

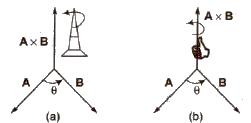
(i) Right Hand Screw Rule Rotate a right handed screw from first vector (A) towards second vector (B). The direction in which the right handed screw moves gives the direction of vector (C).

(ii) Right Hand Thumb Rule Curl the fingers of your right hand from A to B. Then, the direction of the erect thumb will point in the direction of A * B.