Scalar or Dot Product of Two Vectors

Scalar or Dot Product of Two Vectors

The scalar product of two vectors is equal to the product of their magnitudes and the cosine of the smaller angle between them. It is denoted by . (dot).

A * B = AB cos θ

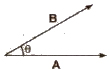
The scalar or dot product of two vectors is a scalar.

Properties of Scalar Product

(i) Scalar product is commutative, i.e., A * B= B * A

(ii) Scalar product is distributive, i.e., A * (B + C) = A * B + A * C.

(iii) Scalar product of two perpendicular vectors is zero.

A * B = AB cos 90° = O

(iv) Scalar product of two parallel vectors is equal to the product of their magnitudes, i.e., A * B = AB cos 0° = AB

(v) Scalar product of a vector with itself is equal to the square of its magnitude, i.e.,

A * A = AA cos 0° = A²

(vi) Scalar product of orthogonal unit vectors

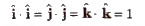
and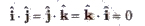 

(vii) Scalar product in cartesian coordinates

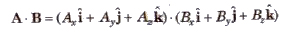
                                               = A_xB_x + A_yB_y + A_zB_z.