ADDITION OF VECTORS

#. Addition of Vectors :-

1. Triangle Law of Vectors

If two vectors acting at a point are represented in magnitude and direction by the two sides of a triangle taken in one order, then their resultant is represented by the third side of the triangle taken in the opposite order.

If two vectors A and B acting at a point are inclined at an angle θ, then their resultant

R = √A² + B² + 2AB cos θ

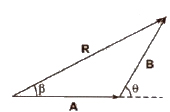
If the resultant vector R subtends an angle β with vector A, then

tan β = B sin θ / A + B cos θ.

2. Parallelogram Law of Vectors

If two vectors acting at a point are represented in magnitude and direction by the two adjacent sides of a parallelogram draw from a point, then their resultant is represented in magnitude and direction by the diagonal of the parallelogram draw from the same point.

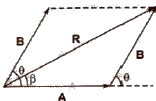
Resultant of vectors A and B is given by

√A² + B² + 2AB cos θ

If the resultant vector R subtends an angle β with vector A, then

tan β = B sin θ / A + B cos θ.

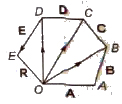
3. Polygon Law of Vectors

It states that if number of vectors acting on a particle at a time are represented in magnitude and direction by the various sides of an open polygon taken in same order, their resultant vector E is represented in magnitude and direction by the closing side of polygon taken in opposite order. In fact, polygon law of vectors is the outcome of triangle law of vectors.

R = A + B + C + D + E

OE = OA + AB + BC + CD + DE

#. Properties of Vector Addition

(i) Vector addition is commutative, i.e., A + B = B + A

(ii) Vector addition is associative, i.e.,

A +(B + C)= B + (C + A)= C + (A + B)

(iii) Vector addition is distributive, i.e., m (A + B) = m A + m B.